Researchers from Ningbo University and Southeast University have designed a hybrid silicon-dielectric-graphene-grating structure, which can modulate the amplitude, wavelength and phase of surface plasmon polaritons (SPPs) simultaneously.

The SPPs are stimulated by the grating and propagating on the graphene, the Fermi level of the graphene is controlled by the voltage applied between silicon substrate and graphene. This structure has potential applications in fields like optical switches, communications and photo-detection.

Gerdau Graphene has announced that Packseven, one of Brazil’s largest flexible film makers, will be commercializing  what they define as 'the world's first graphene-enhanced stretch film'. It is expected to be made available for sale in Q3 2023.

The new ultra-thin film, developed using Gerdau Graphene’s specialized graphene additive technology, is said to be significantly thinner and more durable: initial testing revealed that the new films could pack 120% more material without breaking compared with comparable flexible films. More durable stretch films reduce consumption of the material per pallet and increase safety in packing and loading. 

Researchers from Qatar University (QU), Maimoona Mohamed and Nada Yahya Deyab, along with their supervisor Dr. Shabi Abbas Zaidi, have made progress in addressing the challenge of oil-water separation.

Their research focuses on developing a novel material for efficient oil recovery from oil-water mixtures. By modifying polyurethane (PU) sponges and cotton with reduced graphene oxide (rGO), they have achieved promising results in terms of hydrophobicity, oil-absorption efficacy, reusability, and cost-effectiveness, offering a promising solution to address the issue of water and soil pollution caused by oil spills.

Researchers from Portugal's Instituto de Engenharia de Sistemas e Computadores – Microsistemas e Nanotecnologias (INESC MN), Universidade de Lisboa and the UK's University of Exeter have developed an efficient flexible triboelectric textile by using printed graphene electrodes with polydimethylsiloxane (PDMS) and the textile itself as the triboelectric pair.

To achieve this, the team used a textile planarization technique with a polyurethane adhesive, along with three different deposition methods: graphene droplet films (GDF), graphene immersion films (GIF), and graphene spray films (GSF). 

Versarien has raised £650,000 (over USD$850,000) in a placing for working capital purposes.

The proceeds will be used for working capital purposes and as bridge finance to extend the Company's cash runway ahead of any funds received from asset sales.

Today we published a new edition of our Graphene Oxide Market Report, with all the latest information, including both new research activities. Our market report is a comprehensive guide to graphene oxide (and r-GO) materials and their promising applications in energy storage, composite materials, bio-medical, water treatment and more.

Reading this report, you'll learn all about:

• The difference between graphene oxide and graphene
• Graphene oxide properties
• Possible applications for graphene oxide
• Reduction of graphene oxide to r-GO

The report package also provides:

• A list of prominent GO research activities
• A list of all graphene oxide developers and their products
• Datasheets for over 20 different GO materials
• Free updates for a year

This Graphene Oxide market report provides a great introduction to graphene oxide materials and applications, and covers everything you need to know about GO materials on the market. This is a great guide for anyone interested in applying graphene oxide in their products.

Haydale has reported the completion of stages one and two of a three-stage low-power hot water project in collaboration with Cadent Gas. Haydale said the project, first announced in February 2022, aimed to address the challenge of providing a low-power water heating solution during interruptions to the gas supply, particularly for vulnerable customers such as the elderly or disabled.

During stage one, Haydale said it identified four specific and detailed user case scenarios where their graphene ink-based heaters could be effectively used across Cadent's network. That initial stage helped lay the foundation for subsequent development work, with building on the findings - stage two of the project - focused on creating an operational pre-product prototype. The prototype showcased Haydale's functionalized graphene ink, which is printed onto flexible heater sheets which were then enclosed within an insulated 3D printed portable unit.

Archer Materials has reported the completion of a proof-of-concept biosensing graphene transistor for use in its biochip, and submitted the technology
design to a commercial foundry to verify scalability.

Archer’s optical lithography has electrodes, bond pads, and other graphene componentry, that allow the biochip’s sensor device design to scale more easily to produce complete wafers in collaboration with commercial foundries. The Archer-designed gFET sensing chips will be produced by a commercial foundry, with the aim of Archer validating its design to ensure appropriate scalability for the manufacturing process.

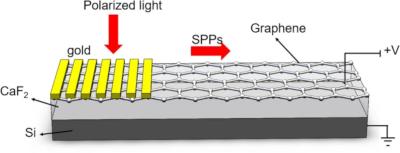
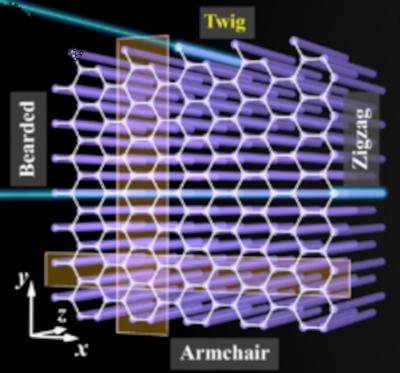
Graphene and graphene-like materials can host—at their edges—localized states whose properties can differ dramatically from those of bulk states. Three types of edge states have been established in these materials—zigzag, bearded, and armchair—named after their geometry. Now, researchers from Nankai University and Shanxi University used a graphene-like photonic crystal to demonstrate the possibility of a fourth edge, called twig, with exotic topological features. Their results may broaden the understanding of graphene edge states, as well as open new avenues for realization of robust edge localization and nontrivial topological phases based on Dirac-like materials.

The team explained that the main findings were that the twig edge is a generic type of honeycomb lattice (HCL) edge complementary to the armchair edge, formed by choosing the right primitive cell (rather than simple lattice cutting or Klein edge modification). In addition, the twig edge states form a complete flat band across the Brillouin zone with zero-energy degeneracy, characterized by nontrivial topological winding of the lattice Hamiltonian. The twig edge states can also be elongated or compactly localized at the boundary, manifesting both flat band and topological features. 

Researchers find a way to make the detection of antibiotic residues in water more quick and simple. The research team included scientists from the Czech Advanced Technology and Research Institute (CATRIN) at Palacký University and the Technical University of Ostrava. The new biosensor looks like a small box connected to a mobile phone. This device can immediately detect even very small antibiotic residues, namely ampicillin, in water or dairy products.

It is based on a tailor-made nanomaterial derived from fluorographene, developed by scientists from the Graphene Flagship Associated Member Czech Advanced Technology and Research Institute (CATRIN) of Palacký University and its Faculty of Science (Czech Republic). They used the so-called click chemistry method, which was awarded the Nobel Prize in Chemistry last year.